Introducción al sensado distribuido por fibra óptica

La infraestructura moderna, desde ductos de energía hasta sistemas de transporte, exige soluciones de monitoreo que ofrezcan cobertura continua, inmunidad electromagnética y largo alcance.

Las infraestructuras relacionadas a la generación, transporte y distribución de energía presentan complejidades particulares a la hora de asegurar su integridad, debido a su extensión que puede alcanzar decenas e incluso miles de kilómetros. Estas estructuras necesitan imperiosamente soluciones de monitoreo que ofrezcan cobertura continua, inmunidad electromagnética y largo alcance.

La tecnología de Sensado Distribuido por Fibra Óptica emerge como una solución ideal al convertir una fibra óptica estándar en una red masiva de sensores distribuidos que miden parámetros físicos a lo largo de decenas de kilómetros. A diferencia de los sensores puntuales, esta tecnología ofrece un perfil de medición continuo y distribuido, permitiendo la localización precisa de eventos anómalos.

El principio de funcionamiento de esta tecnología es el análisis de la luz que se dispersa en sentido contrario (backscattered) al pulso incidente. Existen fundamentalmente tres tipos de sistemas de sensado distribuido, cada uno de ellos basado en un fenómeno de dispersión específico y diseñado para monitorizar un parámetro físico distinto como se resume en la Tabla 1.

Tabla 1. Tipos de Sistema de Sensado Distribuido

Fundamentos de fibra óptica

El funcionamiento de una fibra óptica se basa en el principio de la Reflexión Interna Total (TIR), donde la luz inyectada queda confinada y se propaga en un medio con un índice de refracción más alto (el núcleo) rodeado por un medio con un índice menor (el revestimiento).

Estructura de una fibra óptica:

• Núcleo (Core): El medio por donde se propaga la luz.
• Revestimiento (Cladding): Mantiene la luz confinada dentro del núcleo.
• Recubrimiento (Coating): Protege la fibra de daños mecánicos y humedad.

Figura 1. Estructura de una fibra óptica¹

La forma en que la luz se propaga a través del núcleo define los dos tipos principales de fibra óptica, cada uno con características y aplicaciones distintas:

• Fibras ópticas Monomodo (SMF – Single-Mode Fiber)
  • Modo de Propagación: Permite la propagación de un único modo de luz a través de su núcleo.
  • Tamaños Típicos: El núcleo tiene un diámetro de aproximadamente 8 a 10 µm. El revestimiento estándar es de 125 µm.
  • Longitudes de Onda de Operación: Típicamente utilizadas con láseres en las ventanas de 1310 nm y 1550 nm.
• Fibra Óptica Multimodo (MMF – Multi-Mode Fiber):
  • Modo de Propagación: Posee un núcleo de mayor diámetro, lo que permite que múltiples rayos de luz (modos) se propaguen simultáneamente a través de diferentes caminos dentro del núcleo.
  • Tamaños Típicos: El núcleo puede tener diámetros de 50 µm o 62.5 µm. El revestimiento también suele ser de 125 µm.
  • Longitudes de Onda de Operación: Generalmente operan en longitudes de onda más cortas, como 850 nm y 1300 nm.

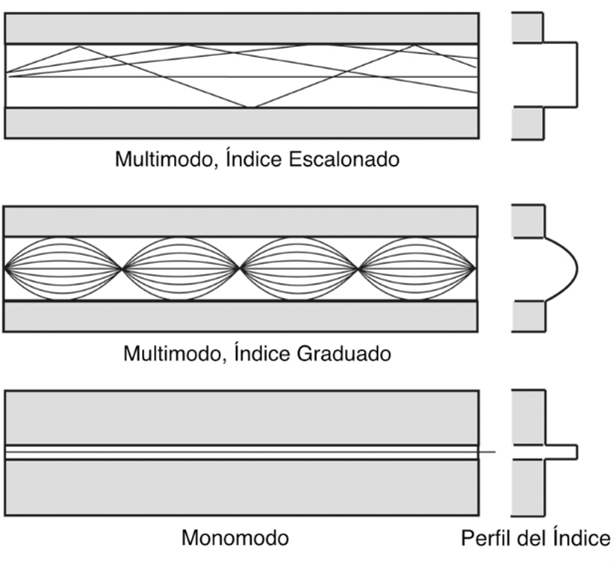
Figura 2. Modos de propagación en fibra óptica²

La elección entre fibra monomodo y multimodo en el diseño de un sistema de sensado distribuido depende directamente del fenómeno de dispersión que se pretende explotar y de las especificaciones de rendimiento requeridas para la aplicación particular.

Las fibras monomodo son críticas para los sistemas DAS y DTSS de alta precisión, donde la coherencia y la estrechez del espectro lumínico son necesarias. Las fibras multimodo son a menudo preferidas en DTS por su mayor apertura numérica, que maximiza el retorno de la señal Raman, aunque también existen algunos sistemas DTS de precisión basados en monomodo.

Fenómenos de retrodispersión y aplicaciones

El sensado distribuido por fibra óptica se basa en el principio de la retrodispersión (Backscattering). Cuando un pulso de luz láser se inyecta en el núcleo de la fibra, la mayor parte de la energía se propaga hacia adelante. Sin embargo, una pequeña fracción de esa luz interactúa con las moléculas y estructuras del vidrio de sílice, siendo dispersada en múltiples direcciones, incluida la dirección contraria, es decir, regresando hacia el equipo interrogador.

La capacidad de un interrogador para detectar, medir el tiempo de viaje de retorno y analizar las características de esta luz dispersada, es lo que permite medir parámetros a lo largo de toda la extensión de la fibra con una resolución espacial precisa.

Existen tres tipos principales de dispersión que se aprovechan en las tecnologías de sensado distribuido: Rayleigh, Brillouin y Raman.

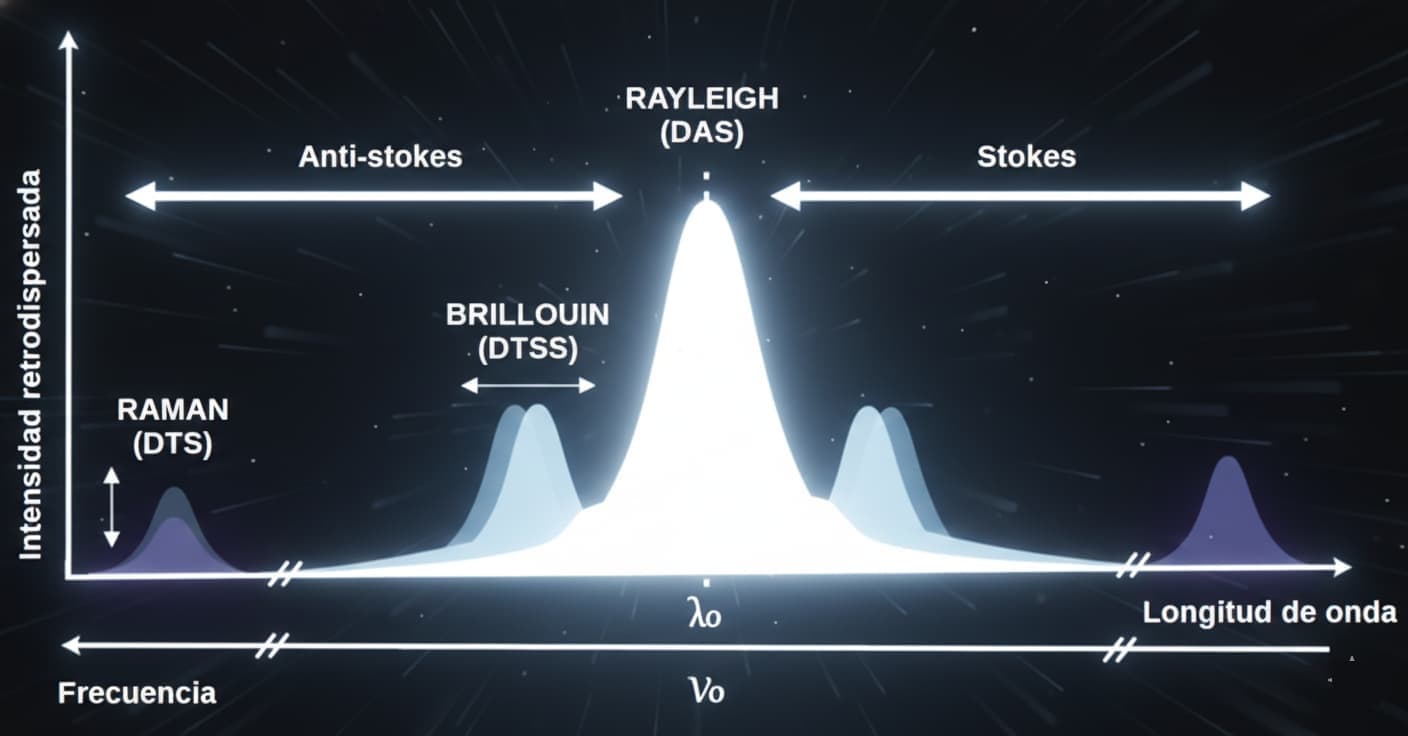
Figura 3. Tipos de dispersión en fibra óptica

Dispersión de rayleigh

Se produce por las fluctuaciones microscópicas y permanentes de densidad del vidrio de sílice. Estas imperfecciones, causadas durante el proceso de fabricación, actúan como pequeños y numerosos puntos reflectores.

La luz dispersada mantiene la misma longitud de onda (frecuencia) que el pulso láser incidente. El sistema de Sensado Acústico Distribuido (DAS) se enfoca en el cambio de fase de la luz Rayleigh de retorno.

Una vibración o una onda acústica externa aplica una deformación local a la fibra. Esta deformación altera la fase de la luz Rayleigh dispersada en ese punto. El sistema DAS actúa como un interferómetro distribuido de alta precisión para detectar y localizar estos eventos acústicos.

El cambio de fase ) en un segmento de fibra de longitud  se describe fundamentalmente como:

\( \Delta\phi = \frac{2\pi}{\lambda} \Delta(nL) \)

∆ϕ: cambio de fase inducido por la perturbación.
λ: longitud de onda de la luz incidente.
Δ(nL): cambio en la longitud óptica del segmento de fibra.

El cambio en la longitud óptica Δ(nL) es el resultado de la deformación (strain) aplicada por la onda acústica, la cual altera dos factores simultáneamente:

• Cambio en el índice de refracción (Δn): La presión de la onda acústica altera la densidad del vidrio de sílice, lo que provoca un cambio Δn (conocido como efecto fotoelástico).
• Cambio en la longitud física (ΔL): La deformación por tensión o compresión estira o comprime el segmento de fibra, provocando un cambio en su longitud.

Un interrogador DAS recupera y demodula este ∆ϕ oscilante, convirtiéndolo en la señal acústica de interés, permitiendo así el monitoreo distribuido a lo largo de toda la fibra.
 

Dispersión de brillouin

La Dispersión de Brillouin se debe a la interacción de los fotones de la luz láser incidente con las ondas acústicas térmicas (llamadas fonones acústicos) que se propagan constantemente en el material de la fibra (vidrio de sílice). Esta interacción resulta en un pequeño desplazamiento de la frecuencia de la luz retrodispersada.

La Frecuencia de Brillouin (\(\nu_B\)) es el cambio o desplazamiento de frecuencia (shift) que experimenta la luz láser incidente al ser retrodispersada. La magnitud de este desplazamiento es directamente proporcional a la velocidad de las ondas acústicas en la fibra, según la siguiente relación fundamental:

\( \nu_B = \frac{2nv_a}{\lambda_0} \)

Donde:

• \(\nu_B\): desplazamiento de frecuencia Brillouin.
• \(n\): índice de refracción efectivo del núcleo de la fibra.
• \(v_a\): velocidad acústica en el material.
• \(\lambda_0\): longitud de onda de la luz incidente en el vacío.

Un cambio de temperatura calienta o enfría el vidrio de sílice modificando la densidad y rigidez del material y, de este modo, directamente la velocidad acústica \(v_a\). Por otra parte, una deformación modifica las dimensiones y la densidad de la fibra cambiando tanto la velocidad acústica \(v_a\) como el índice de refracción n.

Asumiendo pequeños cambios de temperatura y deformación, la ecuación anterior puede reescribirse mediante la siguiente aproximación lineal:

\( \Delta\nu_B = C_T \Delta T + C_\epsilon \Delta\epsilon \)

Donde:

• \( \Delta\nu_B \): cambio en el desplazamiento de frecuencia Brillouin.
• \( C_T \): coeficiente de sensibilidad a la temperatura.
• \( \Delta T \): variación de temperatura.
• \( C_\epsilon \): coeficiente de sensibilidad a la deformación (strain).
• \( \Delta\epsilon \): variación de la deformación mecánica.

Los coeficientes \( C_T \) y \( C_\epsilon \) las sensibilidades calibradas del sistema; representan cuánto cambia la frecuencia de Brillouin por cada unidad de cambio en temperatura o deformación.
Esta característica, donde un aumento de la temperatura o la deformación provoca un aumento detectable en \( \nu_B \) la base de los sistemas DTSS (Distributed Temperature and Strain Sensing) para mediciones distribuidas.
 

Dispersión de raman

La Dispersión de Raman es un fenómeno de dispersión inelástica que se produce por la interacción de los fotones del pulso láser incidente con las vibraciones moleculares del vidrio de sílice (llamadas fonones ópticos). Esta interacción resulta en un cambio significativo de la frecuencia de la luz retrodispersada (mayor que el desplazamiento de Brillouin).

La interacción Raman genera dos bandas de luz secundarias que tienen frecuencias desplazadas respecto a la luz incidente \( \nu_0 \):

• Banda Stokes \( \nu_S \): Los fotones pierden energía al excitar la molécula de sílice. Su frecuencia es menor \( \nu_S < \nu_0 \).
• Banda Anti-Stokes \( \nu_{AS} \): Los fotones ganan energía al chocar con una molécula ya excitada por la energía térmica. Su frecuencia es mayor \( \nu_{AS} > \nu_0 \).

La intensidad de la banda Anti-Stokes \( I_{AS} \) es altamente sensible y aumenta exponencialmente con la temperatura de la fibra, ya que depende de la población de fonones ópticos excitados térmicamente.

Los sistemas DTS (Distributed Temperature Sensing) se basan en la relación entre las intensidades de ambas bandas, ya que solo la banda Anti-Stokes es sensible a la temperatura.

La intensidad de la luz Anti-Stokes \( I_{AS} \) en relación con la luz Stokes \( I_S \) se rige por la distribución de Boltzmann. La relación se expresa mediante la siguiente ecuación:

\( \frac{I_{AS}}{I_S} \approx \left( \frac{\nu_{AS}}{\nu_S} \right)^4 e^{-\frac{h\Delta\nu}{k_B T}} \)

Donde:

• \( I_{AS} \) y \( I_S \): intensidades de las señales Anti-Stokes y Stokes medidas.
• \( \nu_{AS} \) y \( \nu_S \): frecuencias de las bandas Anti-Stokes y Stokes.
• \( h \): constante de Planck.
• \( k_B \): constante de Boltzmann.
• \( \Delta\nu \): desplazamiento de frecuencia entre las bandas.
• \( T \): temperatura absoluta de la fibra (en Kelvin).

Al medir la relación \( I_{AS}/I_S \) se eliminan los efectos indeseables que afectan por igual a ambas señales (como las fluctuaciones de potencia de la fuente, la atenuación de la fibra y las pérdidas en los conectores).

Esto garantiza que la medición final sea una función pura y absoluta de la temperatura \( T \), siendo este el principio fundamental de los sensores DTS.